在图像识别中，并非所有的像素都包含了我们想要的信息。只关注一小部分信息可能对我们更有帮助，即部分信息重要，而部分信息不重要。

在计算机视觉中，我们会将图片通过卷积和池化运算改变其张量形状。在输出张量的维度中，有些是空间维度（宽高），有些是通道维度（颜色、纹理等）。因此注意力可以分为空间注意力和通道注意力。空间注意力强调特征图的空间区域的重要性，如左下角的区域、右上角的区域；通道注意力则强调不同通道的重要性。

1 注意力提示

注意力提示可以分为非自主性和自主性。

非自主性提示基于环境中物体的突出性，在黑白场景中出现一个鲜艳物体自然会不由自主地吸引别人。而自主性提示是我们主动去关注某些重要信息，例如我们在看论文时会相对关注标题、摘要等部分，而不是作者。

自主性和非自主性注意力提示解释了人类的注意力方式，下面我们看看如何通过这两种注意力提示，用神经网络来设计注意力机制的框架。

2 查询、键和值

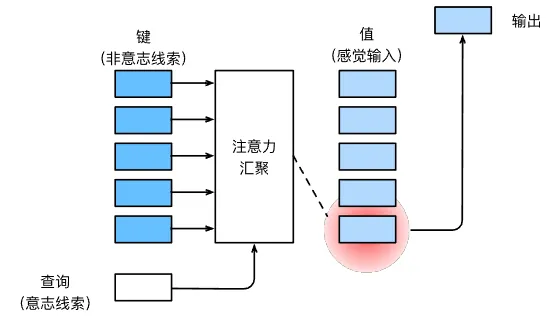
在注意力机制的背景下，自主性提示被称为查询。给定任何查询，注意力机制通过注意力池化将选择引导至感官输入，例如中间特征表示。在注意力机制中，这些感官输入被称为值，每个值都与一个键匹配。

3 注意力池化：以 Nadaraya-Watson 核回归为例

平均池化层可以被视为输入的加权平均值，各个输入的权重相同。而在注意力池化中，各个权重是在给定的查询和不同的键之间计算得出的。

Nadaraya-Wastion 核回归模型是一个简单的例子。考虑下面的回归问题：给定成对的“输入-输出”数据集 $\{(x_1, y_1), \cdots, (x_n, y_n)\}$，如何学习$f$来预测任意输入$x$的输出$\hat{y} = f(x)$？

首先使用最简单的基于平均池化的估计器解决问题。

$$f(x)=\frac{1}{n} \sum_{i=1}^{n} y_i$$

也就是说，对于任意输出，我们只输出一个固定值——这太扯淡了。显然这是由于平均池化忽略了输入$x_i$导致的。

3.1 非参数注意力池化

Nadaraya 和 Watson 基于此，提出根据输入的位置对输出$y_i$进行加权：

$$f(x)=\sum_{i=1}^n \frac{K(x-x_i)}{\sum_{j=1}^n K(x-x_j)} y_i$$

式中$K(u)$为核。我们不讨论核的细节，而是抽象出一个更通用的注意力池化的公式：

$$f(x)=\sum_{i=1}^n \alpha(x,x_i) y_i$$

其中$x$是给定的查询，$(x_i, y_i)$是输入-输出键值对，查询$x$和键$x_i$之间的关系建模为注意力权重$\alpha(x,x_i)$，这个权重将会分配给每个对应值$y_i$。对于任何查询，模型的所有键值对注意力权重都是一个有效的概率分布，即非负且总和为 1。

我们考虑一个高斯核：

$$K(u) = \frac{1}{\sqrt{2\pi}} \exp \left(-\frac{u^2}{2}\right)$$

则：

$$\begin{align*} f(x) &=\sum_{i=1}^n \frac{K(x-x_i)}{\sum_{j=1}^n K(x-x_j)} y_i \\ &=\sum_{i=1}^n \frac{\exp(-\frac{1}{2} (x-x_i)^2)}{\sum_{j=1}^n \exp(-\frac{1}{2} (x-x_i)^2)} y_i \\ &=\sum_{i=1}^n {\rm{softmax}} \left(-\frac{1}{2} (x-x_i)^2\right) y_i \end{align*}$$

在上式中，如果一个键$x_i$越接近给定的查询$x$，那么分配给这个键的对应值$y_i$的注意力权重就会越大，也就是获得了更多的注意力。

3.2 带参数注意力池化

带参数注意力池化拥有一个可学习的参数$w$：

$$\begin{align*} f(x) &=\sum_{i=1}^n \frac{K((x-x_i)w)}{\sum_{j=1}^n K((x-x_j)w)} y_i \\ &=\sum_{i=1}^n \frac{\exp(-\frac{1}{2} ((x-x_i)w)^2)}{\sum_{j=1}^n \exp(-\frac{1}{2} ((x-x_i)w)^2)} y_i \\ &=\sum_{i=1}^n {\rm{softmax}} \left(-\frac{1}{2} ((x-x_i)w)^2\right) y_i \end{align*}$$

4 注意力评分函数

我们刚才使用了高斯核来对查询和键之间的关系进行建模。我们将高斯核的指数部分$-\frac{u^2}{2}$被称为注意力评分函数，上述过程就是对评分函数进行 softmax 运算。

通过这些步骤，我们得到键值对的概率分布（即注意力权重），最后注意力池化输出这些注意力权重的值的加权和。

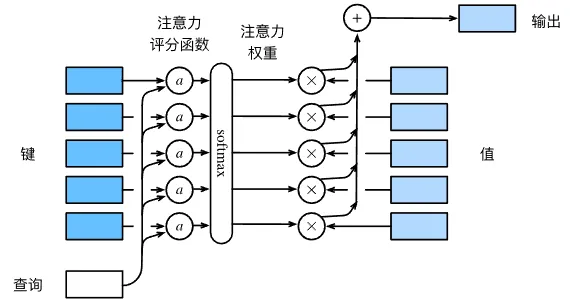
设有一个查询$\boldsymbol{q}$和$m$个键值对$(\boldsymbol{k}_1, \boldsymbol{v}_1), \cdots, (\boldsymbol{k}_m, \boldsymbol{v}_m)$，则注意力池化函数可被表示为：

$$f(\boldsymbol{q}, (\boldsymbol{k}_1, \boldsymbol{v}_1), \cdots, (\boldsymbol{k}_m, \boldsymbol{v}_m)) = \sum_{i=1}^m \alpha(\boldsymbol{q}, \boldsymbol{k}_i) \boldsymbol{v}_i$$

其中查询$\boldsymbol{q}$和键$\boldsymbol{k}_i$的注意力权重是通过注意力评分函数$\alpha$将两个向量映射为标量，再经过 softmax 运算得到：

$$\alpha(\boldsymbol{q}, \boldsymbol{k}_i) = {\rm{softmax}} (a(\boldsymbol{q}, \boldsymbol{k}_i)) = \frac{\exp{a(\boldsymbol{q}, \boldsymbol{k}_i)}}{\sum_{j=1}^m \exp{a(\boldsymbol{q}, \boldsymbol{k}_i)}}$$

因此，选择不同的注意力评分函数$a$将导致不同的注意力池化操作。根据不同的注意力评分函数，可以分为加性注意力和点积注意力。

4.1 加性注意力

当查询和键是长度不同的向量时，可以使用加性注意力作为评分函数：

$$a(\boldsymbol{q}, \boldsymbol{k}) = \boldsymbol{w}_v^T \tanh (\boldsymbol{W}_q \boldsymbol{q} + \boldsymbol{W}_k \boldsymbol{k})$$

其中$\boldsymbol{W}_q$、$\boldsymbol{W}_k$和$\boldsymbol{w}_v$是在训练过程中可学习的参数。

4.2 点积注意力

当查询和键是相同长度$d$的向量时，我们可以使用效率更高的点积注意力：

$$a(\boldsymbol{q}, \boldsymbol{k}) = \boldsymbol{q}^T \boldsymbol{k}$$

当维度过高时，点积值可能会过大，因此我们有缩放点积注意力：

$$a(\boldsymbol{q}, \boldsymbol{k}) =\frac{\boldsymbol{q}^T \boldsymbol{k}}{\sqrt{d}}$$

再加入小批量，我们就得到了基于查询 $\boldsymbol{Q}_{n \times d}$、键 $\boldsymbol{K}_{m \times d}$和值 $\boldsymbol{V}_{m \times v}$ 的缩放点积注意力：

$${\rm{softmax}} \left( \frac{\boldsymbol{Q} \boldsymbol{K}^T}{\sqrt{d}} \right) \boldsymbol{V}$$

其中$v$为值的长度。