神经网络之所以得名，是因为其中的参数相互连接，形成类似于神经系统一样的网状结构。在之前我们实现的线性回归和 softmax 回归并非严格意义上的神经网络，因为其只有一层。

softmax 回归在结构上是对输入做线性变换后再通过 softmax 函数得到概率分布，但其本质仍然是线性模型，无法处理复杂的非线性关系。

而在这里我们将会学习真正的深度神经网络。最简单的深度神经网络称为多层感知机。它由多层神经元组成，每一层从它的上一层接收输入，又向下一层输出。

这一节我们会学习更多的基础概念，如隐藏层和激活函数。

1 多层感知机的数学基础

线性回归和 softmax 回归都是线性模型。但是这个世界并不总是线性的。我们需要寻找一些变换来突破线性模型的限制。例如，我们可以在输入和输出之间添加一个或者多个函数，使其能处理更普遍的函数关系类型，也就是隐藏层。

我们以图的方式描述多层感知机。

图示的多层感知机共有两层（输入层不计入，因为输入层不参与计算）。假设两层均为线性模型，那么：

对于从输入层到隐藏层，有

$$\boldsymbol{H} = \boldsymbol{X} \boldsymbol{W}_1 + \boldsymbol{b}_1$$

对于从隐藏层到输出层，有

$$\boldsymbol{O} = \boldsymbol{H} \boldsymbol{W}_2 + \boldsymbol{b}_2$$

不难发现最终输出$\boldsymbol{O}$仍然是输入$\boldsymbol{X}$的线性函数。那么这使得隐藏层失去了原本的意义——我们想引入隐藏层以突破线性模型的限制。

这启发我们，在隐藏层处理结束后，应该对结果应用非线性函数，以保证多层感知机不会退化为线性模型。这个非线性函数称为激活函数。

为了构建更通用的多层感知机，我们可以继续堆叠隐藏层。通过简单隐藏层的堆叠，实现对复杂函数的精确模拟。理论上，具有足够隐藏单元的一层感知机就能逼近任意连续函数；而多层结构则可以用更少的神经元，更高效地表示复杂函数。

1.1 ReLu 函数及其导数

修正线性单元（ReLU）提供了一种非常简单的非线性变换。

$${\rm ReLU}(x) = \max \{x, 0\}$$

它的导数为

$$\frac{\rm d}{{\rm d}x} {\rm ReLU}(x) = \left\{ \begin{aligned} 0, x \leq 0 \\ 1, x \gt 0 \\ \end{aligned} \right.$$

提示

事实上，根据严格的数学定义，ReLU 函数在 0 处的导数不存在。但是我们可以忽略这种情况，因为输入可能永远都不为 0。在深度学习领域内，“如果微妙的边界条件很重要，那么我们很可能是在研究数学而非工程”。

1.2 sigmoid 函数及其导数

对于一个定义域为全体实数的函数，挤压函数（sigmoid）可以将输入变换为$(0,1)$上的输出。

$${\rm sigmoid}(x) = \frac{1}{1+\exp(-x)}$$

它的导数为

$$\frac{\rm d}{{\rm d}x} {\rm sigmoid}(x) = \frac{\exp(-x)}{(1+\exp(-x))^2} = {\rm sigmoid}(x)(1- {\rm sigmoid}(x))$$

1.3 tanh 函数及其导数

与 sigmoid 函数类似，双曲正切函数（tanh）可以将全体实数上的输入变换为$(-1,1)$上的输出。

$$\tanh(x) = \frac{1-\exp(-2x)}{1+\exp(-2x)}$$

它的导数为

$$\frac{\rm d}{{\rm d}x} \tanh(x) = 1-\tanh^2 (x)$$

2 从框架实现多层感知机

我们还是以 softmax 回归时用的 Fashion-MINST 数据集训练。

与 softmax 的框架实现相比，唯一的区别就是在定义网络时添加了一层 ReLU 函数和一层线性层。

net = nn.Sequential(
    nn.Flatten(),
    nn.Linear(784, 256),
    nn.ReLU(),
    nn.Linear(256, 10),
)

其他部分完全一致。

可以看到，在经过 10 轮训练后，损失函数和准确率都比 softmax 回归好很多。

epoch 1, train loss 1.046, train acc 0.634, test acc 0.717
epoch 2, train loss 0.603, train acc 0.789, test acc 0.777
epoch 3, train loss 0.522, train acc 0.818, test acc 0.812
epoch 4, train loss 0.481, train acc 0.833, test acc 0.830
epoch 5, train loss 0.452, train acc 0.841, test acc 0.834
epoch 6, train loss 0.434, train acc 0.847, test acc 0.832
epoch 7, train loss 0.416, train acc 0.853, test acc 0.838
epoch 8, train loss 0.405, train acc 0.857, test acc 0.808
epoch 9, train loss 0.391, train acc 0.862, test acc 0.826
epoch 10, train loss 0.382, train acc 0.864, test acc 0.855

那我们继续叠加激活函数，训练表现会不会更好呢？很遗憾，并不会。简单堆叠层数并不总是带来性能提升。

net = nn.Sequential(
    nn.Flatten(),
    nn.Linear(784, 256),
    nn.ReLU(),
    nn.Linear(256, 128),
    nn.ReLU(),
    nn.Linear(128, 10)
)

epoch 1, train loss 1.860, train acc 0.299, test acc 0.526
epoch 2, train loss 0.914, train acc 0.652, test acc 0.613
epoch 3, train loss 0.691, train acc 0.750, test acc 0.750
epoch 4, train loss 0.590, train acc 0.788, test acc 0.799
epoch 5, train loss 0.527, train acc 0.811, test acc 0.810
epoch 6, train loss 0.489, train acc 0.824, test acc 0.802
epoch 7, train loss 0.458, train acc 0.835, test acc 0.834
epoch 8, train loss 0.433, train acc 0.843, test acc 0.838
epoch 9, train loss 0.417, train acc 0.849, test acc 0.821
epoch 10, train loss 0.403, train acc 0.855, test acc 0.827

3 过拟合和泛化误差

我们的训练目标是想要模型从有限的数据中学习到一类通用的模式，以对未知数据进行预测，即前面提到的泛化。

上面提到过继续叠加激活函数并不会使训练效果更好，反而会出现过拟合现象。当模型在训练数据上拟合的比在潜在分布中更接近时，我们说发生了过拟合。

可以这么简单理解，过拟合就像一个死记硬背练习题的学生，当考试时出现他从没见过的题目时，就会无所适从。

当神经元、层数、迭代次数足够多时，模型最终可以在训练集上达到完美的精度，但是在测试集上的准确性却下降了，即发生了过拟合。

我们使用泛化误差讨论过拟合的程度。泛化误差是指，模型应用在同样从原始样本的分布中抽取的无限多数据样本时，模型误差的期望。

由于我们不可能收集到无限多的样本，因此实际上我们从数据集中抽取一部分来估计泛化误差，也就是验证集。和测试集一样，验证集也是随机选取、与训练集不能产生重合部分。

因此我们的数据会被分成三份：训练集、验证集和测试集。在我们确认所有的超参数之前，不应该使用测试集。

4 正则化和权重衰减

对抗过拟合的方法称之为正则化，权重衰减是最广泛使用的正则化技术之一。

权重衰减通过计算函数与 0 的距离来衡量函数的复杂度。一种简单的方法是通过线性函数 $f(\boldsymbol{x}) = \boldsymbol{w}^T \boldsymbol{x}$ 中权重向量 $\boldsymbol{w}$ 的 $L_2$ 范数的平方 $||\boldsymbol{w}||^2$ 来度量其复杂度。

例如对于线性回归模型的损失函数：

$$L(\boldsymbol{w}, b) = \frac{1}{n} \sum_{i=1}^n \frac{1}{2} \left( \boldsymbol{w}^T \boldsymbol{x}_i + b - y_i \right)^2$$

加入对权重向量 $\boldsymbol{w}$ 的惩罚项：

$$L(\boldsymbol{w}, b) + \frac{\lambda}{2}||\boldsymbol{w}||^2$$

这里的系数 $\frac{1}{2}$ 是为了求导后能使系数为 1。$\lambda$ 是一个新的超参数正则化常数，它用于限制 $||\boldsymbol{w}||$ 的大小。

PyTorch 中已经集成了权重衰减模块，以线性神经网络为例，要加入权重衰减，只需要：

optimizer = torch.optim.SGD([
    {'params': net[0].weight, 'wd': wd},
    {'params': net[0].bias, 'lr': lr}
])

这里采用数组形式，是因为偏置参数$b$并不参与到正则化中来，因此我们选择对权重和偏置分别设置超参数。在调用时中传入wd参数即可。

5 暂退法

我们先来思考一下什么是一个好的深度学习模型。我们希望这个模型能在未知的数据上也有较好的预测表现，并且对于相同或者相似的输入能得到相同或者相似的输出，也就是平滑性。例如当我们对图像进行分类时，向图像内加入一些随机噪声应该是基本无影响的。因此有人提出一个想法：在训练过程中，在后续计算层之前向网络的每一层注入噪声。因为当训练一个多层的神经网络时，注入噪声只会在输入-输出映射上增强平滑性。这个想法就是暂退法。

从表面上看，在每次训练迭代过程中，暂退法在计算下一层之前将当前层中的一些节点置零，也就是丢弃某些神经元。

在标准暂退法正则化中，每个中间值 $h$ 以暂退概率 $p$ 被随机变量 $h'$ 替换，即：

$$h' = \left\{ \begin{aligned} 0, \text{概率为}p \\ \frac{h}{1-p}, \text{其他情况} \\ \end{aligned} \right.$$

这样在替换后，整层的期望保持不变，即 $E[h'] = h$。

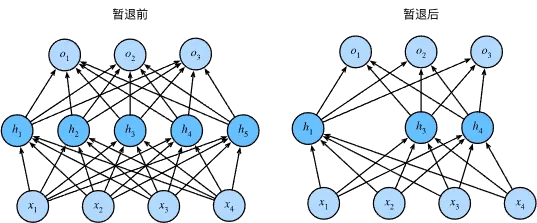
经过暂退法处理后，可以有效避免模型过度依赖某一神经元的情况，提高平滑性。

对于 PyTorch，我们只需要在每个全连接层之后添加一个Dropout层，并传入暂退概率即可：

net = nn.Sequential(
    nn.Flatten(),
    nn.Linear(784, 256),
    nn.ReLU(),
    nn.Dropout(p1) # 第一次暂退
    nn.Linear(256, 128),
    nn.ReLU(),
    nn.Dropout(p2) # 第二次暂退
    nn.Linear(128, 10)
)