Part 1 卷积神经网络基本原理
约 3129 字大约 10 分钟
2025-08-01
多层感知机非常适合表格数据。然而对于图像这种多维数据,这种缺少结构的网络并不适用。
在 softmax 回归的例子中,我们使用的是 28×28 像素的图片,这样每次输入就高达 784 维。当我们遇到 1000×1000 像素的照片时,输入就高达 100 万维。这几乎等同于不可能了。
因此我们需要一种新的网络来处理图片这种数据。
1 卷积神经网络的数学基础
设想我们要从人群里找到某一特定的人,我们无论用何种方法找到他,都应该和他的所处位置无关,也就是平移不变性。而目标的特征和环境无关,我们只需要计算一小部分的图像即可,也就是局部性。
基于这两个性质,我们可以将这个图片分割成多个区域,并使用一个检测器逐区域扫描,并输出每个区域中出现目标的可能性。
多层感知机输入一个二维图像 X,其隐藏层为一个二维张量 H。我们用 [X]i,j 和 [H]i,j 表示对应位置的像素,将权重矩阵替换为四阶张量 W。假设偏置参数为 U,则全连接层可以表示为:
[H]i,j=[U]i,j+k∑l∑[W]i,j,k,l[X]k,l=[U]i,j+a∑b∑[V]i,j,a,b[X]i+a,j+b
其中k=i+a,l=j+b。[W] 和 [V] 具有一一对应关系。索引a和b在偏移过程中覆盖了整个图像。
由于平移不变性,检测对象在输入 X 中的平移应该仅导致隐藏层 H 中的平移。也就是说 V 和 U 与像素坐标 (i,j) 无关。即 [V]i,j,a,b=[V]a,b,且 U 是一个常数。于是有
[H]i,j=u+a∑b∑[V]a,b[X]i+a,j+b
这就是卷积,我们使用系数 [V]a,b 对位置 (i,j) 附近的像素加权得到 [H]i,j。
接着我们加入局部性。根据局部性的描述,我们不应该关注距离 (i,j) 较远位置的信息。也就是在 ∣a∣>Δ 或 ∣b∣>Δ之外,[V]a,b=0。
[H]i,j=u+a=−Δ∑Δb=−Δ∑Δ[V]a,b[X]i+a,j+b
上述推导过程中输入的是一个二维图像,然而我们常见的图像包含三个通道,即R、G、B。因此我们的输入、输出都要调整为三维张量。
为了能够表示输入 X 和隐藏层 H 中的多个通道,我们可以给 V 中添加两个坐标,即 [V]a,b,c,d。其中 c 为输入通道索引,d 为输出通道索引。综上:
[H]i,j,d=u+a=−Δ∑Δb=−Δ∑Δ[V]a,b,c,d[X]i+a,j+b,c
2 卷积层
2.1 互相关运算
严格来说,卷积是个错误的叫法,它所表达的运算其实是互相关运算。根据我们之前的描述,在卷积层中,输入张量和核张量通过互相关运算产生输出张量。
我们先忽略输入通道的情况,在这个 3×3 的二维图像张量中,卷积核的大小为 2×2。在二维互相关运算中,卷积窗口从输入张量的左上角开始,从左至右、从上至下滑动。 当卷积窗口滑动到新一个位置时,包含在该窗口中的部分张量与卷积核张量进行按元素相乘,得到的张量再求和得到一个单一的标量值,由此我们得出了这一位置的输出张量值。
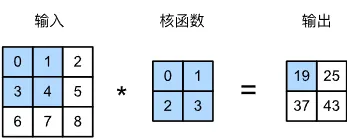
例如输出张量左上角的 19 来源于:
19=0×0+1×1+3×2+4×3
2.2 简单的目标边缘检测
我们设计一个简单的卷积应用,通过找到像素变化的位置,来检测图像中不同颜色的边缘。
例如对于一幅 6×8 的黑白图像X,我们构造一个高度为 1、宽度为 2 的卷积核K。当进行互相关运算时,如果水平两元素相同,则输出为 0,否则不为 0。
X = tensor([[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.]])
K = tensor([[1., -1.]])然后我们定义一个互相关操作函数:
def corr2d(X, K):
h, w = K.shape
Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
return Y将输入X和卷积核K输入函数中,即可得到操作结果:
tensor([[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.]])2.3 学习卷积核
在实际应用中我们不可能手动设计卷积核,因此我们需要通过训练得到能适用于复杂图像的卷积核。
正如我们训练线性神经网络时一样,我们先构造一个卷积层,然后将卷积核初始化为随机张量,接着迭代、计算梯度、更新卷积核。
PyTorch 提供了二维卷积层,我们可以直接使用:
# 构造一个二维卷积层,它具有 1 个输出通道和 1×2 的卷积核
conv2d = nn.Conv2d(1, 1, kernel_size=(1, 2), bias=False)
# 这个二维卷积层使用四维输入和输出格式(批量大小、通道、高度、宽度),
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
lr = 3e-2
for i in range(10):
Y_hat = conv2d(X)
l = (Y_hat - Y) ** 2
conv2d.zero_grad()
l.sum().backward()
# 迭代卷积核
conv2d.weight.data[:] -= lr * conv2d.weight.grad
if (i + 1) % 2 == 0:
print(f'epoch {i+1}, loss {l.sum():.3f}')
print(f'卷积核:{conv2d.weight.data.reshape((1, 2))}')得到的卷积核为:
tensor([[ 1.0307, -0.9488]])2.4 特征映射和感受野
卷积层可以被视为一个输入映射到下一层的空间维度的转换器,因此也被称为特征映射。
在卷积神经网络中,对于某一层的任意元素x,其感受野是指在前向传播期间可能影响计算的所有元素(来自所有先前层)。
请注意,感受野可能大于输入的实际大小。以我们上边体积的 2×2 卷积核为例,阴影输出元素值 19 的感受野是输入阴影部分的四个元素。假设之前输出为 Y,其大小为 2×2,现在我们在其后附加一个卷积层,该卷积层以 Y 为输入,输出单个元素 z。在这种情况下,Y 上的 z 的感受野包括 Y 的所有四个元素,而输入的感受野包括最初所有九个输入元素。
因此,当一个特征图中的任意元素需要检测更广区域的输入特征时,我们可以构建一个更深的网络。
2.5 填充
卷积后的图像尺寸缩小一些。可以证明,若输入图像的形状为 nh×nw,卷积核的形状为 kh×kw,则卷积后图像的尺寸为
(nh−kh+1)×(nw−kw+1)
因此当我们进行多层卷积时,边缘像素会严重丢失。为了缓解这种情况,我们常常在图像边缘填充一些值为 0 的像素。
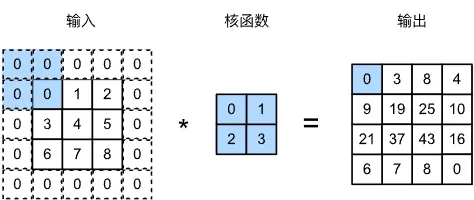
当高度填充和宽度填充分别为 ph 和 pw 时,输出图像的尺寸为
(nh−kh+ph+1)×(nw−kw+pw+1)
因此,当我们需要得到和输入尺寸相同的输出时,只需要设置 ph 和 pw 分别为 kh−1 和 kw−1 即可。
PyTorch 提供了填充的实现:
nn.Conv2d(1, 1, kernel_size=3, padding=1) # 在所有侧边填充 1 个像素
nn.Conv2d(1, 1, kernel_size=3, padding=(2, 1)) # 在高度上填充 2 个像素,在宽度上填充 1 个像素2.6 步幅
卷积核每次滑动的距离称为步幅。我们之前使用的都是长度为 1 的步幅。有时为了高效计算,或者为了降低采样次数,我们可以使卷积核跳过部分像素,每次滑动多个像素。
例如这是水平步幅为 2,垂直步幅为 3 的结果:
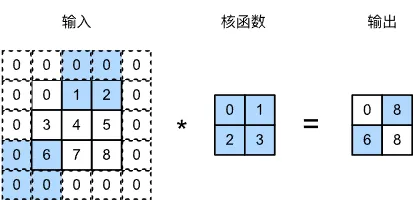
容易计算,当垂直步幅和水平步幅分别为 sh 和 sw 时,输出图像的尺寸为
⌊shnh−kh+ph+sh⌋×⌊swnw−kw+pw+sw⌋
PyTorch 同样提供了步幅的实现:
nn.Conv2d(1, 1, kernel_size=3, padding=1, stride=2) # 步幅为 2
nn.Conv2d(1, 1, kernel_size=3, padding=1, stride=(3, 4)) # 垂直步幅为 3,水平步幅为 42.7 通道
2.7.1 多输入通道
当我们添加通道时,输入图像就变成了一个三维张量,它的大小为
h×w×c
对于最常见的 RGB 图像,c 为 3。
当输入包含多个通道时,需要构造一个相同通道数量的卷积核,以便对多个通道进行互相关运算。因此对于 ci 通道图像,其卷积核大小为
kh×kw×ci
例如一个双通道图像的双通道卷积核:
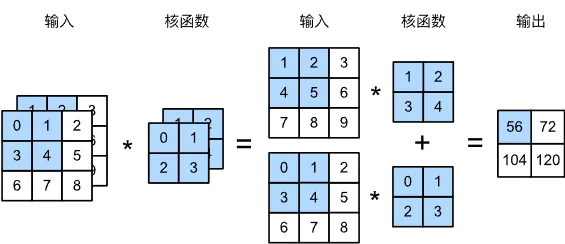
2.7.2 多输出通道
有时我们希望得到多个输出通道,每个通道代表不同的输出响应,如边缘、纹理、形状等。每次卷积都是在降低输入图像的大小,同时我们可以增加输出通道的数量,以捕捉更多更复杂的抽象特征。
为了获得多个通道的输出,我们可以为每个输出通道创建一个卷积核。每个卷积核对原始图像进行计算得到对应通道的输出。
这样卷积核的大小为
kh×kw×ci×co
4 池化层
我们在上边提到了感受野。在卷积神经网络中,我们希望随着网络层数加深,逐步降低特征图的空间分辨率,从而聚合信息、扩大感受野,让神经元对更大的图像区域作出响应。这种做法可以让网络最终具备对整张图像进行全局判断的能力,
然而,现实中图像往往存在位置偏移(如拍摄角度、抖动等),我们不希望模型对这些微小变化过于敏感。因此,我们除了使用卷积操作,还会引入池化层(也称汇聚层)来进一步降低空间分辨率,加快模型计算,提取更稳定的特征(如边缘、角点),并增强网络的平移不变性,降低对图像中物体具体位置的敏感性。
4.1 最大池化与平均池化
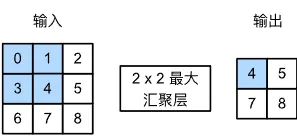
与卷积层类似,池化运算符也是一个固定形状的窗口。与卷积核不同的是,池化运算没有参数,而是计算窗口中所有元素的最大值或平均值,分别称为最大池化和平均池化。
例如最大池化:
PyTorch 提供了最大池化层和平均池化层,可以直接使用。
4.2 填充和步幅
与卷积层一样,池化层也可以通过填充和步幅改变输出形状。默认情况下,PyTorch 中的步幅和池化窗口的大小相同。
nn.MaxPool2d(3) # 最大池化,池化窗口为 3,步幅为 3
nn.MaxPool2d(3, padding=1, stride=2) # 最大池化,池化窗口为 3,填充为 1,步幅为 2
nn.AvgPool2d((2, 3), padding=(0, 1), stride=(2, 3)) # 平均池化,池化窗口为 2×3,高度填充 0,宽度两侧填充 1,垂直步幅为 2,水平步幅为 34.3 通道
在处理多通道数据时,池化层在每个输入通道上单独运算,并不会在输出通道中汇总。因此池化层的输出通道和输入通道数量相同。