LeNet 是最早发布的卷积神经网络之一，因其在计算机视觉任务中的高效性能而受到广泛关注。LeNet 在 1989 年被 Yann LeCun 提出并命名。

1 LeNet 结构

LeNet 由卷积编码器和全连接层稠密块两部分组成：

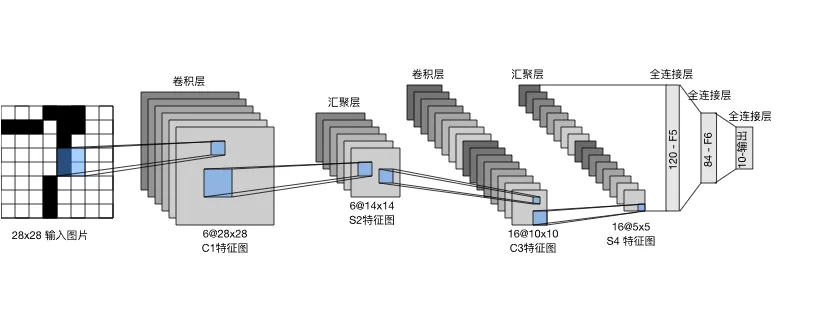
卷积编码器保罗两个卷积块，每个卷积块的基本单元是一个卷积层、一个 sigmoid 激活函数和一个平均池化层。每个卷积层使用 5×5 卷积核和一个 sigmoid 激活函数，将输入映射为多个通道的输出。第一卷积层有 6 个输出通道，第二卷积层有 16 个输出通道。每个 2×2 池化层将尺寸降低为原来的四分之一。

然后传递给全连接层稠密块。我们将这个四维输入转换成全连接层所期望的二维输入。这里的二维表示的第一个维度索引小批量中的样本，第二个维度给出每个样本的平面向量表示。LeNet 的稠密块有三个全连接层，分别有 120、84 和 10 个输出。因为我们在执行分类任务，所以输出层的 10 维对应于最后输出结果的数量。

2 LeNet 的 PyTorch 实现

使用 PyTorch 框架可以非常简单地实现 LeNet：

# 定义网络
net = nn.Sequential(
    # 第一卷积块
    nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    # 第二卷积块
    nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    # 全连接层稠密块
    nn.Flatten(),
    nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.Sigmoid(),
    nn.Linear(84, 10))

# 初始化模型参数
def init_weights(m):
    if type(m) == nn.Linear or type(m) == nn.Conv2d:
        nn.init.xavier_uniform_(m.weight)

net.apply(init_weights)

完整代码为：

import torch
from torch import nn
from torch.utils import data

import torchvision
from torchvision import transforms


def load_data_fashion_mnist(batch_size):
    # 将 Fashion-MNIST 数据集转换为 Tensor
    trans = [transforms.ToTensor()]
    trans = transforms.Compose(trans)

    minst_train = torchvision.datasets.FashionMNIST(
        root="data/FashionMNIST", train=True, transform=trans, download=True
    )

    minst_test = torchvision.datasets.FashionMNIST(
        root="data/FashionMNIST", train=False, transform=trans, download=True
    )

    train_iter = data.DataLoader(minst_train, batch_size, shuffle=True)

    test_iter = data.DataLoader(minst_test, batch_size, shuffle=False)

    return train_iter, test_iter


def accuracy(y_hat, y):
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
        y_hat = y_hat.argmax(axis=1)
    cmp = y_hat.type(y.dtype) == y
    return float(cmp.type(y.dtype).sum())


def evaluate_accuracy(net, data_iter, device):
    if isinstance(net, torch.nn.Module):
        net.eval()

    metric = [0.0, 0.0]  # [正确预测数, 总样本数]

    with torch.no_grad():
        for X, y in data_iter:
            X, y = X.to(device), y.to(device)
            y_hat = net(X)
            metric[0] += accuracy(y_hat, y)
            metric[1] += y.numel()

    return metric[0] / metric[1]


def train(lr, num_epochs, train_iter, test_iter, device):
    # 定义LeNet神经网络结构
    net = nn.Sequential(
        nn.Conv2d(1, 6, kernel_size=5, padding=2),
        nn.Sigmoid(),
        nn.AvgPool2d(kernel_size=2, stride=2),
        nn.Conv2d(6, 16, kernel_size=5),
        nn.Sigmoid(),
        nn.AvgPool2d(kernel_size=2, stride=2),
        nn.Flatten(),
        nn.Linear(16 * 5 * 5, 120),
        nn.Sigmoid(),
        nn.Linear(120, 84),
        nn.Sigmoid(),
        nn.Linear(84, 10),
    )

    # 初始化模型参数
    def init_weights(m):
        if type(m) == nn.Linear or type(m) == nn.Conv2d:
            nn.init.xavier_uniform_(m.weight)

    net.apply(init_weights)

    # 将模型移动到指定设备
    net.to(device)

    # 定义损失函数：交叉熵损失
    loss = nn.CrossEntropyLoss()

    # 定义优化器：小批量随机梯度下降
    optimizer = torch.optim.SGD(net.parameters(), lr=lr)

    # 训练循环
    num_batches = len(train_iter)

    for epoch in range(num_epochs):
        # 设置为训练模式
        net.train()

        # 用于统计本epoch的训练指标
        train_loss = 0.0
        train_acc = 0.0

        for i, (X, y) in enumerate(train_iter):

            X, y = X.to(device), y.to(device)
            optimizer.zero_grad()
            y_hat = net(X)
            l = loss(y_hat, y)
            l.backward()
            optimizer.step()

            # 累积损失和准确率
            train_loss += l.item()
            train_acc += accuracy(y_hat, y)

            if (i + 1) % 100 == 0:
                print(
                    f"Epoch [{epoch + 1}/{num_epochs}], Step [{i + 1}/{num_batches}], Loss: {l.item():.4f}"
                )

        # 计算本epoch的平均训练损失和准确率
        train_loss /= num_batches
        train_acc /= len(train_iter.dataset)

        # 在测试集上评估模型
        test_acc = evaluate_accuracy(net, test_iter, device)

        # 打印epoch结果
        print(f"Epoch [{epoch + 1}/{num_epochs}] 完成")
        print(
            f"训练损失: {train_loss:.4f}, 训练准确率: {train_acc:.4f}, 测试准确率: {test_acc:.4f}"
        )

    return net


def predict(net, test_iter, device, num_samples=10):
    text_labels = [
        "t-shirt",
        "trouser",
        "pullover",
        "dress",
        "coat",
        "sandal",
        "shirt",
        "sneaker",
        "bag",
        "ankle boot",
    ]

    net.eval()

    # 获取一个batch的测试数据
    X, y = next(iter(test_iter))
    X, y = X.to(device), y.to(device)

    with torch.no_grad():
        y_hat = net(X)
        predicted = y_hat.argmax(axis=1)

    # 显示前num_samples个样本的预测结果
    print(f"预测结果展示（前{num_samples}个样本）：")
    for i in range(min(num_samples, len(y))):
        true_label = text_labels[y[i].item()]
        pred_label = text_labels[predicted[i].item()]
        print(
            f"样本 {i+1}: 真实标签: {true_label}, 预测标签: {pred_label}, "
            f"{'✓' if y[i] == predicted[i] else '✗'}"
        )

    # 计算整体准确率
    overall_acc = evaluate_accuracy(net, test_iter, device)
    print(f"\n测试集整体准确率: {overall_acc:.4f}")


if __name__ == "__main__":
    # 超参数设置
    batch_size = 256  # 批量大小
    lr = 0.9  # 学习率
    num_epochs = 10  # 训练轮数
    
    device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

    # 加载数据
    train_iter, test_iter = load_data_fashion_mnist(batch_size)

    # 训练模型
    net = train(lr, num_epochs, train_iter, test_iter, device)

    # 进行预测
    predict(net, test_iter, device)