神经网络的设计模式从一开始的单个神经元角度思考问题，再发展到整个层，再发展为块、重复层的模式。

使用块的想法首先出现在牛津大学的视觉几何组（Visual Geometry Group）的 VGG 网络中。通过使用循环和子程序，可以很容易地在任何现代深度学习框架的代码中实现这些重复的架构。

1 VGG 块与 VGG 网络

经典卷积神经网络的基本组成部分是这样的：

• 带填充以保持分辨率的卷积层；
• 激活函数，如 ReLU；
• 池化层。

而一个 VGG 块与之类似，由一系列卷积层组成，再加上用于空间下采样的最大池化层。

与 AlexNet 和 LeNet 一样，VGG 网络可分为两部分：卷积层和池化层组成的第一部分、全连接层组成的第二部分。通过堆叠 VGG 块，并加上数层全连接层，即形成了 VGG 网络。

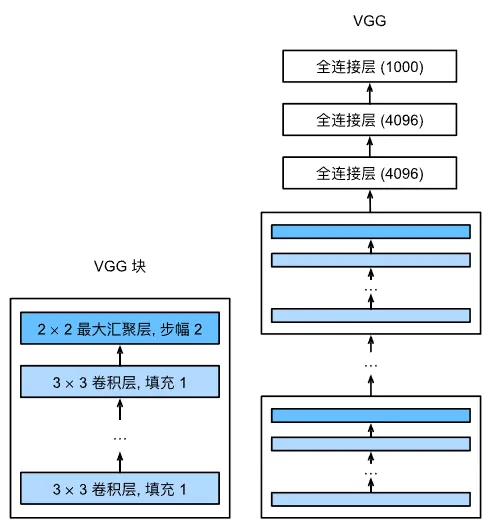
原始的 VGG 网络有 5 个卷积块，前两个块各有一个卷积层，后三个块各有两个卷积层。由于该网络使用 8 个卷积层和 3 个全连接层，因此它通常被称为 VGG-11。

VGG-11 的 5 个卷积块中，第一个模块有 64 个输出通道，后续每个模块将通道数量翻倍，直至最后一层的 512 个输出通道。

2 VGG-11 的 PyTorch 实现

我们知道一个 VGG 块由数层卷积层和一个池化层组成，因此我们只需要指定卷积层数、输入通道数和输出通道数即可。通过循环，可以轻易创建出我们想要的 VGG 块。

def vgg_block(num_convs, in_channels, out_channels):
    layers = []
    for _ in range(num_convs):
        layers.append(nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1))
        layers.append(nn.ReLU())
        in_channels = out_channels

    layers.append(nn.MaxPool2d(kernel_size=2, stride=2))

    return nn.Sequential(*layers)

VGG-11 每个卷积块中卷积层数和输出通道数分别为：

块	卷积层数	输出通道数
1	1	64
2	1	128
3	1	256
4	2	512
5	2	512

然后我们使用 for 循环实现：

def vgg(conv_arch):
    conv_blks = []
    in_channels = 1
    # 卷积层部分
    for num_convs, out_channels in conv_arch:
        conv_blks.append(vgg_block(num_convs, in_channels, out_channels))
        in_channels = out_channels

    return nn.Sequential(
        *conv_blks,
        nn.Flatten(),
        # 全连接层部分
        nn.Linear(out_channels * 7 * 7, 4096),
        nn.ReLU(),
        nn.Dropout(0.5),
        nn.Linear(4096, 4096),
        nn.ReLU(),
        nn.Dropout(0.5),
        nn.Linear(4096, 10)
    )

conv_arch表明了 VGG 各卷积块结构，传入参数即可得到 VGG-11 网络。

conv_arch = ((1, 64), (1, 128), (2, 256), (2, 512), (2, 512))
net = vgg(conv_arch)

VGG-11 对于 MNIST 太复杂了，因此我们降低各卷积层层通道数量到原来的四分之一，得到一个较小的网络。

conv_arch = ((1, 16), (1, 32), (2, 64), (2, 128), (2, 128))
small_net = vgg(conv_arch)

将学习率调整到 0.05，其他训练过程与 AlexNet 基本一致。